Prerequisites:

• Basic Knowledge of Functions / Methods

• Knowledge of Memory Management

So, basically, have you ever tried writing long code for a simple logic problem using functions? Then here comes the recursion to help you reduce the lines of code.

Recursion is simply a technique used to break down problems into parts and solve them one by one. Let’s imagine a scenario in which a mom asks her son to count his total number of fingers, and he tells her the count.

While the kid is having a problem counting, his father comes and helps him by splitting the problems one by one. The easy and less time-consuming solution is to count fingers on one hand, and then add that to counting your fingers on the other hand.

The same thing happens when it comes to solving a problem using recursion in programming. The definition is a function that calls itself to solve a problem.

Let’s get deep into this now.

Firstly, we all know that when a function gets called, it gets stored in stack memory. When the function completes its execution, it is removed from the stack.

Let’s take an example and try to understand how the recursion also helps to not repeat the work again and again. You have to print your name five times. It seems easy, right? But here is the cache:

• You have to print using a function,

• not to use any loops,

• not to call the function five times.

It seems somewhat difficult, right? Let me help you here.

public class RecEx_1 {
    public static void main(String[] args) {
        fun1("My Name!");
    }
    static void fun1(String name){
        System.out.println(name);
        fun2(name);
    }
    static void fun2(String name){
        System.out.println(name);
        fun3(name);
    }
    static void fun3(String name){
        System.out.println(name);
        fun4(name);
    }
    static void fun4(String name){
        System.out.println(name);
        fun5(name);
    }
    static void fun5(String name){
        System.out.println(name);
    }
}

Here, we are just calling one function from the main function. But the output is five times greater. It is happening because we are also calling another function within a function.

Basically, it works something like this internally:

The function fun1 is called from the main function with a string as an argument, printing the argument as it is. The function fun1 is calling the function fun2 with the argument that it got from the main function fun1. The function fun2 prints its parameter and calls the next function fun3 with the argument that it got from function fun1. The rest of the functions repeat themselves.

But when it comes to the function fun5, it doesn’t call any other function. It means we are stopping the function calls from function fun5, because we have to print five times the argument into a function.

Can’t you see something wrong over here—that we are repeating a lot of work here? We are using the printing default function five times, passing the same argument five times, and calling the functions.

As we had discussed before, recursion also helps us not just split the problem into parts and solve it but also not repeat things in code.

Let’s try to optimize this code,

public class RecEx_2 {
    public static void main(String[] args) {
        fun("Hello", 5);
    }

    static void fun(String name, int n) {
        if (n <= 0) {
            return;
        }
        System.out.println(name);
        fun(name, n-1);
    }
}

We got it, we are using a variable that indicates the number of times that the string should be printed. We also perform a few basic elementary mathematical operations here, like decrementing the variable value by one whenever we print the argument.

At the beginning of the function, we set up a condition that says that if the variable’s value is less than or equals 0, then we have to stop the function's execution. It is called the base condition.

If we observe the last line of the function block, we are calling the same function with the same argument but decrementing the variable’s value. It gets updated to the 4 and the 3, 2, 1, 0. When it reaches zero, it stops the execution and returns to the main function. And also, we get our work done with just five lines of code.

We have just called the same function by performing a few operations on parameters and setting the base condition. It is recursion!

Let us try to solve a few questions and understand more about the recursion.

Printing the numbers from N to 0 and 0 to N

Solution: “ I suggest you solve the problem before watching the solution here.”

public class Rec_EX3 {
    public static void main(String[] args) {
        OnetoN(0);
        System.out.println("-------------------");
        NtoOne(10);
    }
    static void OnetoN(int n){
        if (n>=10){
            return;
        }
        System.out.println(n);
        OnetoN(n+1);
    }
    static void NtoOne(int n){
        if (n==0){
            return;
        }
        System.out.println(n);
        NtoOne(n-1);
    }
}

If you get the same answer or solution without any errors, congratulations! Otherwise, don’t worry. Here, we should set up the base condition for sure. Else, we may get an error like this.

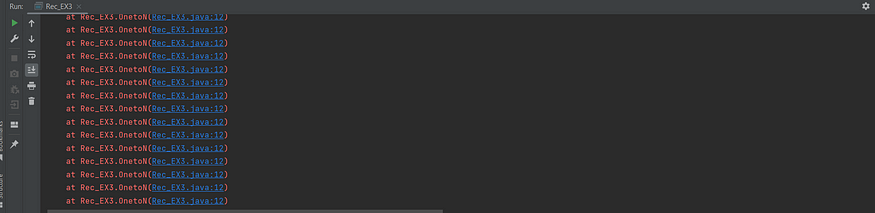
Error while solving Recursion

This function does not have a base condition and will keep calling itself indefinitely. If you call function OnetoN in the main method, the program will continue to print "This is an infinite loop!" forever, and the program will eventually crash due to running out of stack space. Hence, it is important to set a base condition.

Then, how do we set the base condition? Simple, the condition is how many times or up to when, you need to call the function itself to produce the output.

Let us try to understand this more using another problem called the Fibonacci Number. Here, we are just trying to print the answer directly, not its total sequence.

Solution:

Try to think of the logic to get the answer using recursion. Here, we have to just decrement the number by one, and by two, we have to add both, and repeat this until we get zero, right?

Let us try to generalize this more. Here we get the number from the main function as an argument. We just add the numbers, which are decremented by one and two.

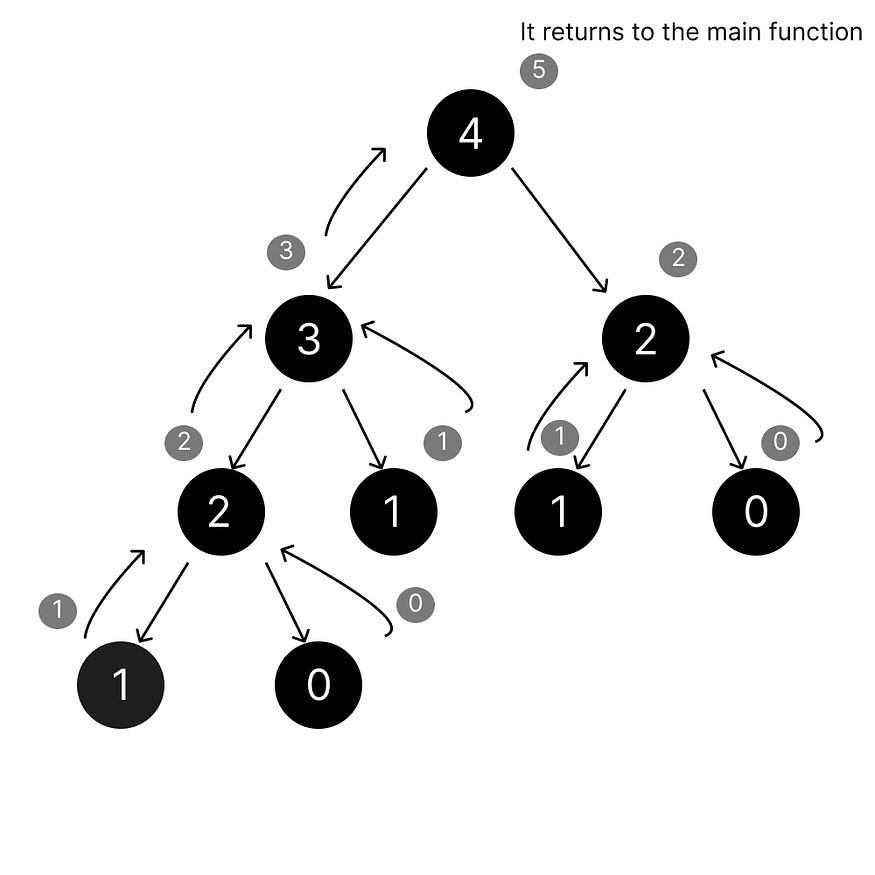
Recursive tree for Fibonacci Number

The Fibonacci of 0 and 1 is 0 and 1, which means these both are less than 2, right?

First, the function is called the fibo(n-1) function. Here, it decrements to fibo(n-1). It repeats until we get 0 or 1. When it gets 0 or 1, it returns the Fibonacci of it.

The sum of all the numbers is passed to the parent function. Like, the sum of 0 and 1 Fibonacci is passed to 2, then to 3, and then to 4.

We are adding this fibo(n-1) function to the fibo(n-2) function, right? The same thing happens here. After the execution, it passes the summation to the function, and when the base condition gets true, it simply returns to the main function, where we store and print the answer.

Stack point of view while running recursion for Fibonacci

Here, once each function returns its value, it gets removed from the stack.

The function fun(n-2), that is, fibo(0), returns 0, so it can be removed from the stack.

Once the whole answer was returned, then the whole function, which is fibo(4), could be removed from the stack. As we all know, after the completion of all commands, the main function also gets removed from the stack, and it would be empty.

public class FiboRec {
    public static void main(String[] args) {
        int ans = fibo(3);
        System.out.println(ans);
    }
    static int fibo(int n){
        if(n <=2){
            return n;
        }
        return fibo(n-1)+fibo(n-2);
    }
}

Here, you might get doubt why the program just can’t return the functions fibo(n-1) and fibo(n-2) separately.

Well, here is a simple explanation for that. In the return statement, we are not just calling a single function. We are calling the two functions, and we just return the addition of those two after the completion of their execution.

It’s not just like printing the numbers from 0 to n. Here we just call the single function; it is tail recursion. When it comes to Fibonacci using recursion, that’s not the case.

In this problem, we encountered a statement called fibo(n-1)+ fibo(n-2). It is known as the recurrence relation.

How do I find any recursion problems?

• Identify if you can break the problem into parts or not.

• Write the recurrence relation if needed.

• Draw the recursion tree

• About the tree: See the flow of functions, and how they are getting into the stack.

• Identify and focus on left tree calls and right tree calls.

• Tips: Draw the tree and pointer, again and again, using pen and paper.

• Use the debugger feature in IDE to observe how the flow is occurring internally.

If you have learned something new or this article has helped you revise a concept, then please like this article and save it for future reference. If it is possible, please also make a tweet about this, and don’t forget to tag me with @yoursmanjunadh.

In upcoming articles, we are going to solve a few more questions from the leetcode and also help you get familiar with the recursion.